Exciting news! This is the best possible Boggle board:

Boggle is a word search game. You form words by connecting adjacent letters, including along diagonals. Longer words score more points. Good words on this board include STRANGERS and PLASTERING. After you spend three minutes trying to find as many words as you can, you’ll be struck by just how good computers are at this.

Using the ENABLE2K word list, this board has 3,625 points on it coming from 1,045 words. This board has more points than any other. Try any other combination of letters and you’ll get a lower score. While I’ve long suspected this board was the winner, I’ve now proven it via exhaustive search.

Many people have searched for high-scoring boards before, but no one has ever constructed a computational proof that they’ve found the best one. This is a new, first of its kind result for Boggle.

To see why this is interesting, let’s go back to the 1980s.

High-Scoring Boggle and Local Optima

With the release of the Apple II (1977) and IBM PC (1981), computers become accessible to hobbyists, including word game enthusiasts. In 1982, Alan Frank published a short article in Word Ways magazine called High-Scoring Boggle. It’s the earliest work I’ve found on Boggle maximization, and it’s instructive on why this is a hard problem.

Here’s what he wrote:

The article goes on to list the 769 words that add up to 2,047 points. You can browse the words on that board using the fifth edition of OSPD here: gnisetrpseacdbls. (Thanks to the addition of new words, it’s increased to 2,226 points.)

The article doesn’t explain how Alan and Steve came up with this particular board, but I suspect they used a hill climbing procedure. The idea is simple: start with a random board and find its score. Tweak a letter and see if the score improves. If so, keep it. If not, discard the change. Repeat until you stall out. You’ll eventually wind up with a high-scoring board.

Writing a Boggle solver and finding this board was a real achievement in 1982. But unfortunately for Alan and Steve, their board is not “the highest-scoring one.” It’s not even close. The board pictured at the top of this article scores 3,736 points using OSPD5, vastly more than theirs.

So what went wrong? It’s hard to say without their code, but I have a hunch. The bane of hill climbing is the local maximum:

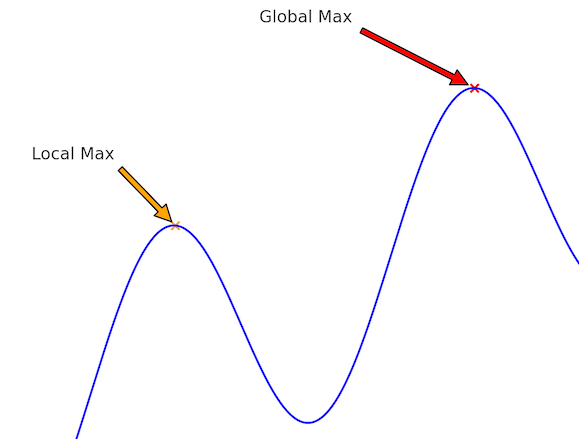
It’s easy for a hill climber to find a local max, rather than the global max. Presumably Alan and Steve’s board is locally optimal, and small changes can’t improve it. But there’s still a much better board out there, you just have to descend your small hill first before you can climb a taller one. Local optimization can always fail in this way. You may just be looking in the wrong neighborhood.

Deeper searches

I wrote my first Boggle Solver in 2004 and quickly got interested in using hill climbing and simulated annealing to find high-scoring boards. I wasn’t the only one.

Boggle programs in the 2000s had some major advantage over Alan and Steve’s from 1982. Memory was much cheaper, CPUs were much faster, and the internet made it much easier to get word lists.

This meant that you could do “deeper” searches:

• Instead of changing just one cell at a time, expand the search radius by changing 2, 3, or 4.
• Instead of tracking just a single best board, track hundreds of high-scoring candidates.
• Instead of doing just a handful of hillclimbing runs, do millions.

Using a process like this, I found that, whatever board I started with, I always wound up with one of a handful of high-scoring boards, including our favorite 3,625 pointer.

This suggested that this board might just be the global max. But still, we could be falling into the same trap as before. The true global optimum might just be hard to find this way.

The only way to know for sure is via exhaustive search. And unfortunately, at least at first glance, this seems completely impossible.

The Impossibility of Exhaustive Search

There are an astronomically large number of possible Boggle boards. How many? If any letter can appear in any position, then there are roughly

26^16/8 = 5,451,092,862,428,609,257,472 = 5.45*10^21

possible boards. (The factor of 8 comes from symmetry; not all boards can be rolled with real Boggle dice, but this is within an order of magnitude.)

It’s possible to find all the words on a Boggle board very quickly using a Trie data structure. On my M2 Macbook, I can score around 200,000 boards/sec. Still, at that pace, testing every board would take around 800 million years!

Fortunately, there’s a more clever way to structure the search.

Branch and Bound

There are just too many boards to look at each one. Even enumerating all of them would be too slow. Instead, we need to group boards together into a “board class.” Then we can calculate an upper bound on the highest-scoring board in each class. If this upper bound is lower than 3625, we can toss out the entire class without having to test any of the individual boards in it. If not, we need to split the class and try again.

This technique is known as Branch and Bound, and it was first developed way back in the 1960s. B&B is more of a strategy than a concrete algorithm, and it leaves a lot of details to fill in. The clever bits of applying this approach to Boggle are:

1. An appropriate way to partition the space of Boggle boards into board classes
2. An upper bound that’s fast to compute but still reasonably “tight”
3. A way to split board classes and calculate their upper bounds without repeating work

A “board class” might contain trillions of individual boards. An example would be boards with a particular consonant/vowel pattern. There are roughly 2^16/8=8192 possible consonant/vowel patterns—vastly fewer than the number of boards. And you can imagine that it’s easy to rule out boards with all consonants or all vowels. Other patterns are much harder, though. (My search didn’t exactly use consonants and vowels, this is just an illustration.) For more on board classes, read this post.

The second and third ideas required developing a somewhat novel tree structure tailor-made for Boggle. These “sum/choice” trees make it efficient both to calculate upper bounds and to split board classes. You can see examples of these trees and read about how they work in this post.

If you’d like to learn more about these algorithm and data structures, I’d encourage you to run the code on your own machine and read some of my previous blog posts, which go into much greater detail:

• Boggle Revisited: Finding the Globally-Optimal 3x4 Boggle Board
• Boggle Revisited: New Ideas in 2025
• Boggle Revisited: A Thrilling Insight and the Power of Algorithms
• Boggle Revisited: Following up on an insight

The results

I developed and tested the search algorithm on 3x3 and 3x4 Boggle, which are much easier problems. Then I ran it on 4x4 Boggle.

Using a 192-core c4 on Google Cloud, it took about 5 days to check around 1 million 4x4 board classes (~23,000 CPU hours). This is about $1,200 of compute. That’s a lot, but it’s not a crazy amount. (Fortunately I had a friend in BigTech with CPUs to spare.)

The result was a list of all the Boggle boards (up to symmetry) that score 3500+ points using the ENABLE2K word list. There were 32 of them. Here are the top five:

• plsteaiertnrsges (3625 points)
• splseaiertnrsges (3603 points)
• gntseaieplrdsees (3593 points)
• dresenilstapares (3591 points)
• dplcseainrtngies (3591 points)

You can see the rest here. These boards are rich in high-value endings like -ING, -ER, -ED, and -S.

The top boards were all ones that I’d previously found by hillclimbing.

What did we learn about the problem?

• Hill Climbing Works. If you search deeply enough, the globally optimal Boggle board can be found via hill climbing and simulated annealing. This doesn’t come as a huge surprise: the space of Boggle boards is “smooth” in that making small changes to one high-scoring board tends to give you another high-scoring board. But this is hand-wavy, and now we know for sure!
• This is NP-Hard. Finding the highest-scoring board in a board class is likely an NP-Hard problem. Fortunately, N is small (4x4=16) and the tailor-made code is able to solve this orders of magnitude faster than general ILP solvers.

Questions and Answers

• Does this use AI? It’s 2025, and yet this project made very little use of AI. The runtime is classic data structures and algorithms, all CPU and no GPU. GitHub Copilot was helpful for translating parts of the Python prototype to C++ and for small coding tasks.
• Can this board be rolled with real Boggle dice? Yes. (See photo for proof!) All the highest-scoring boards can be rolled with both old (pre-1987) and new Boggle dice. My search included all combinations of letters, not just the ones that could actually be rolled.
• What are your odds of rolling this board? Vanishingly low! I believe they’re around 1 in 10^19, which is in the ballpark of the number of stars in the universe. You’re better off playing the lottery.
• What about the letter Q? One of the Boggle dice has a “Qu” on it, and my search allowed any of the cells to be “Qu”. Not surprisingly, the highest-scoring boards had no Qu on it. For ENABLE2K, the best board I’m aware of containing a Qu is cinglateperssidq (3260 points), where the Qu is a dead cell. The best I know of that actually uses the Qu is gepsnaletiresedq (3199 points), which contains QUEER, QUEEREST, etc.
• What about other wordlists? The best board depends on the dictionary you use. There are some slight variations, for example the best board for the OSPD Scrabble Dictionary is likelysplseaiertnrsges (3827 points), which is the second-best board for ENABLE2K (3603 points). The GitHub repo has a breakdown by wordlist. Only the result for ENABLE2K has been proven.
• What are the other high-scoring boards? Here’s a complete list of boards with 3500+ points using ENABLE2K. Many of these are one or two letter variations on each other, but some are quite distinct.
• Why did this happen now? This could have been done at any point in the last 10–20 years. But it was easier today because of the widespread availability of cloud computing. It also helped that I had some free time to devote to this problem.
• Can this be GPU accelerated? People have been asking me about this since 2009. While it’s possible that there’s some version of Boggle that can be GPU accelerated, this isn’t it. The algorithm is too tree-y and branchy. There’s lots of coarse parallelism available, but very little fine-grained parallelism.
• What about other (human) languages? I’ve only run this for English, but you’re welcome to try running the code yourself for other languages. I hear Polish Boggle is interesting!

What tools were used?

The code is a mixture of C++ for performance-critical parts and Python for everything else. They’re glued together using pybind11, which I’m a big fan of.

If you’d like to run the code or learn more, check out the GitHub repo.

What if there’s a bug?

I’d cry. 😭 While I’d never rule out the possibility of a bug, there several reasons to believe that this computational proof is correct:

1. It matches the highest-scoring boards found by exhaustive search on 2x2 and 2x3 Boggle, where this is feasible.
2. It matches the highest-scoring boards found by exhaustive search within a single board class for 3x4 Boggle.
3. It finds all the best boards that I’ve found via hill climbing for 3x3, 3x4 and 4x4 Boggle.
4. The tree operations preserve an invariant on the score that suggests they are valid.

What’s next?

I have a few more ideas for incremental optimizations. But I’ve been hacking away at this problem for at least three months, and this seems like a good place to stop. I wasn’t sure that 4x4 Boggle would ever be “solved” in this way, and it’s immensely satisfying to knock out a problem that’s been in the back of my mind for nearly 20 years.

I do intend to write a paper explaining what I’ve done more formally, as well as another post with my thoughts on this whole experience.

The top-scoring boards for other word lists still need to be proven. Hasbro also sells a 5x5 and 6x6 version of Boggle. These are astronomically harder problems than 4x4 Boggle, and will likely have to wait for another generation of computers and tools. The best board I’ve found via hillclimbing for 5x5 Boggle is sepesdsracietilmanesligdr. The results of this exploration suggest there’s a good chance this is also the global optimum.