08.16.09
Posted in personal at 10:44 am by danvk
I rode a cab to Joe and Amy’s wedding yesterday. It cost $5.05. In a rare moment of innumeracy, I handed the driver a $20 bill and asked for $16 in change. (I’d meant to ask for $14.)
In the confusion that ensued, I wound up paying $5 for my ride to an unhappy cab driver and got out before realizing what had happened. I felt terrible — my cabbie karma was at zero.
On the ride home, I resolved to do better. It was $6.15, so I gave the driver a $10 and asked for $2 back. He handed me a single bill. I was about to complain when I noticed that it was a $2 bill. A sure sign that my cabbie karma had been restored!
Permalink
08.11.09
Posted in boggle at 9:01 pm by danvk
Hopefully the last boggle post for a while! I figured I should throw up a few more examples while I still have time left on my OmniGraffle trial.
There are two main shortcomings to the max/no mark upper bound:
- It can’t keep track of which words it’s already found.
- It can’t keep track of which choices it’s made on each cell.
These can both be fixed, but only by incurring great computational complexity. Remember the tradeoff between the “tightness” of a bound and the difficulty of computing it?
Our first example:
Let’s look at the search tree starting with the “t” cell. There are three possible words: “tar”, “tie” and “tier”. Here’s the search tree that max/no mark generates:
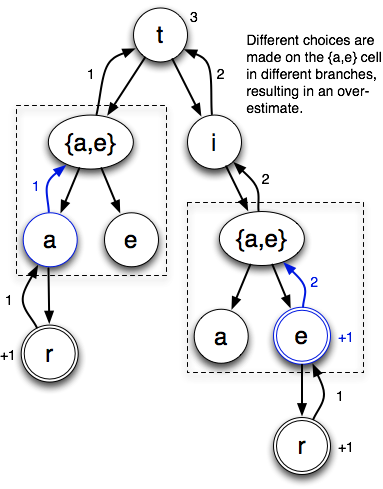
(I’m drawing the trees slightly differently than I did in the last post, to make the branching more explicit. Branches inside dotted lines come from multiple possibilities on a cell. Other branches result from the ordinary process of looking in different directions from a cell.)
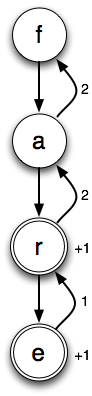
In this example, max/no mark chooses the “a” when it gets to the “{a,e}” cell directly from the “t”. This makes sense, since it results in one point to the e’s zero. However, when it gets to the “{a,e}” cell through the “ti”, it chooses the “e”. This also makes sense, since it gets two points from the “e” (“tie” and “tier”) vs. zero from the “tia” prefix. By the time it makes this choice, it has no memory of choosing the “a” the last time it encountered this cell. If it did, since the “tie” prefix results in two points to the “ta” prefix’s one, it would make sense to go back and change that choice. But remembering this would require lots of expensive bookkeeping. It’s faster (but yields a looser bound) if we just accept the possibility that we’ll make different choices.
Example number 2 of max/no mark’s failings:
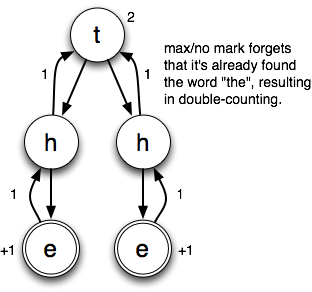
The problem in this case is that max/no mark doesn’t remember which words it’s already found. At first glance, it seems like this problem would be easy to remedy. And it certainly would on this board, in which each cell only has a single possible letter. But if you think about a board with lots of choices, you’ll start to see why it’s best to just give up and accept a looser bound.
Permalink
Posted in boggle at 1:41 pm by danvk
After the last post, several people mentioned that they were confused about how the “max/no mark” upper bound on the highest score in a class of Boggle boards worked. With some help from OmniGraffle, I’ve created some instructive examples.
Here’s a class of boards:
The dots mean “no letters here”. The class contains two different boards:
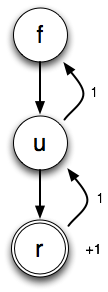
It contains two boards. The one with an “a” has two points worth of words on it, while the one with a “u” only has one. (We’re only looking at words starting with ‘f’ here.)
The diagrams show that the solver starts with the ‘f’ on each board and explores adjacent cells. When it finds a word, it scores it and passes the total score back up the depth-first search tree.
Here’s how the max/no mark bound sees that board class:
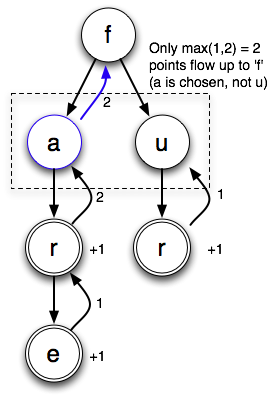
When it gets to the “{a,u}” cell, it tries both possible letters. The “a” tree brings back 2 points, whereas the “u” tree brings back 1 point. So it chooses “a” and counts two points. As it so happens, this is the score of the highest-scoring board. The sum/union bound would have added the 1 and the 2, resulting in an upper bound of 3. The max/no mark bound takes advantage of the fact that this cell can only be one of two possibilities, not both.
Now what if we throw a few more letters on:
With the new letters, there are more points coming from the u:
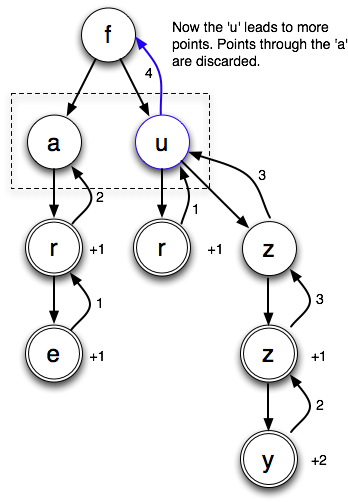
The two points going through the ‘a’ are dropped on the floor. sum/union would have resulting in a bound of 4+2. When there are lots of letter choices on every cell, you can see why max/no mark is a much tighter bound.
It’s important to note that there are two sources of branching in these search trees: (1) being able to go in multiple directions from a cell (i.e. f->u->r or z) and (2) having multiple choices on a cell (i.e. f->a or u). The max/no mark bound sums the scores resulting from choices in case (1) and takes the max of choices in case (2). The sum/union bound takes the sum in both cases.
Permalink
08.08.09
Posted in boggle, math, programming at 10:35 am by danvk
Why is finding the highest-scoring Boggle board so difficult? It’s because there are so many boards to consider: 2^72 for the 4×4 case and 2^40 for the 3×3 case. At 10,000 boards/second the former corresponds to about 2 billion years of compute time, and the latter just two years. Just enumerating all 2^72 boards would take over 100,000 years.
So we have to come up with a technique that doesn’t involve looking at every single board. And I’ve come up with just such a method! This is the “exciting news” I alluded to in the last post.
Here’s the general technique:
- Find a very high-scoring board (maybe this way)
- Consider a large class of boards
- Come up with an upper bound on the highest score achieved by any board in the class.
- If it’s lower than the score in step #1, we can eliminate all the boards in the class. If it’s not, subdivide the class and repeat step #2 with each subclass.
Classes of Boards
By “class of boards”, I mean something like this:
| {a,e,i,o,u} |
{a,e,i,o,u} |
r |
| {b,c,d,f,g,h} |
a |
t |
| d |
e |
{r,s,t,v} |
The squares that contain a set of letters can take on any of those letters. So this board is part of that class:
and so is this:
All told, there are 5 * 5 * 6 * 4 = 600 boards that are part of this class, each with its own score. Other fun classes of boards include “boards with only vowels” (1,953,125 members) and “boards with only consonants” (794,280,046,581 members).
Follow me past the fold for more…
Read the rest of this entry »
Permalink
08.04.09
Posted in boggle at 6:18 pm by danvk
There is exciting news to report in the land of Boggle!
Last we spoke about Boggle, we used Simulated Annealing to get at the question “what is the highest-scoring Boggle board?”
We found a board with 3625 points on it this way. It would have been nice to say that it was the best of all possible boards, but that would have been too rash. While it is a very good board and I have never seen a higher-scoring one, that doesn’t mean there isn’t one out there. Maybe I’ve just been looking in the wrong places.
To prove that the 3625-pointer is the best board, we’d need to show that every other board scores fewer points. In a previous post, I estimated that there were 2^69 possible boggle boards. At 10,000 boards/second, this would take 1.9 billion years of compute time!
When you run up against a computationally intractable problem, there are a few standard ways to deal with it:
- Give up.
- Come up with a brilliant new algorithm to solve the problem more quickly.
- Solve a simpler problem.
Option 1 is the easiest. Option 2 is the hardest. And option 3 is the compromise we’ll be taking for the next few danvk.org boggle posts. Our simpler problem today: 3×3 boggle.
If we drop seven letters (4×4 – 3×3 = 7), we’re left with only 26^9 / 8 ≅ 2^39 boards to consider. If we can achieve 10,000 boards/sec, this would be just over two years’ worth of computation. That’s still a lot, but it’s much more reasonable than 1.9 billion years!
I believe I have solved the 3×3 boggle problem using an approach that is only slightly more clever than this. I used simulated annealing to find very high-scoring 3×3 boards. This was the best one I found, along with its 4×4 best board buddy:
It’s worth noting that the optimal 3×3 board has a 2×3 region in common with the 3625 point 4×4 board.
In the next post we’ll talk about how I showed that this board was higher-scoring than all 2^39 others in significantly less than two years (it took one day). As a teaser, I’ve included all the 3×3 boards with more than 500 points worth of words below the fold.
Read the rest of this entry »
Permalink