02.12.07

Google Ski Trip

Posted in personal at 11:07 pm by danvk

Google’s semi-famous annual ski trip was this past week at Squaw Valley, near Tahoe. Being a midwesterner, I’m still not totally used to this whole “mountain” concept. I checked the weather the night before the trip, and saw that it’d be a high of 45 in Tahoe that day. So warm! Would I even need a coat? Apparently it never occurred to me that weather conditions on the top of a mountain might be different than on the bottom.

Needless to say, I was woefully underprepared. No gloves, no earmuffs, no hat, no ski goggles, etc. So this is what it looks like at the top:

Or rather, that’s what it looked like later. There was a blistering snow storm at first. Run #1 down the bunny slope was the scariest thing I’ve ever done. I had to go down the hill squinting because it was painful to open my eyes and have the snow slam into them. There were some enterprising capitalists selling ski supplies up there, so this is what I looked like shortly thereafter:

I’m second from the right. Much better! Click through for more pictures from Ryan.

Permalink Comments off

02.11.07

Some Boggle Statistics

Posted in boggle at 10:46 pm by danvk

With a fast boggle solver in hand, it’s time for some fun statistics. These are all based on boggle boards rolled with real boggle dice. I’m going sans-code this time, but if you’re interested in seeing it, feel free to holla.

Most common words:

3 letters			4 letters			5 letters
Word	Freq (%)		Word	Freq (%)		Word	Freq (%)
toe	19.258		teen	6.718		eaten	2.034
tee	19.074		tees	6.564		enate	2
ten	17.944		tent	6.02		sente	1.954
net	17.944		note	5.976		setae	1.944
tea	17.65		tone	5.838		tense	1.86
set	17.51		teat	5.804		tease	1.856
eta	17.176		toes	5.664		teeth	1.788
ate	17.176		toea	5.548		eater	1.788
tae	16.518		nets	5.432		teens	1.712
eat	16.518		test	5.344		seton	1.702
tie	16.432		rete	5.208		notes	1.702
het	15.684		nett	5.204		tents	1.646
ret	15.108		nest	5.174		retie	1.632
eth	14.938		tens	5.172		steno	1.624
oes	14.698		sent	5.156		sheet	1.618
the	14.542		neat	5.146		ester	1.618
eon	14.474		etna	5.144		oaten	1.61
one	14.366		ante	5.144		teats	1.608
ose	13.82		thee	5.064		tones	1.606
see	13.78		tote	5.052		enter	1.596

I looked these words up and they all check out. See the Scrabble dictionary if you’re not convinced.

How many words can we expect to find on each board?

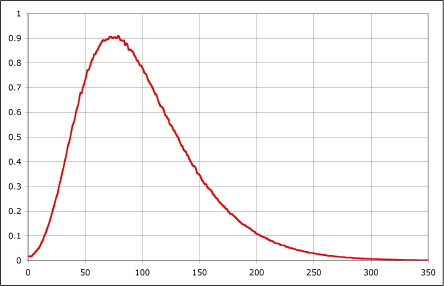
That looks like a log-normal distribution. The mean is 98.53 words. How many points?

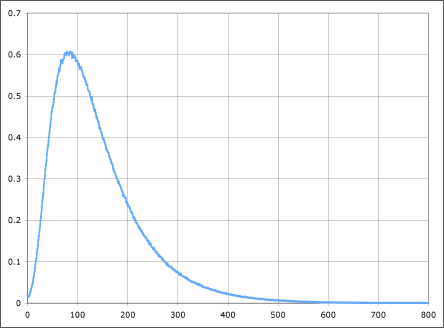
That’s also a log-normal distribution with the characteristically long tail. The mean is 140.97 points per board.

How many words of each length can we expect to find on a board? Here’s a histogram of the number of words of each length on a board:

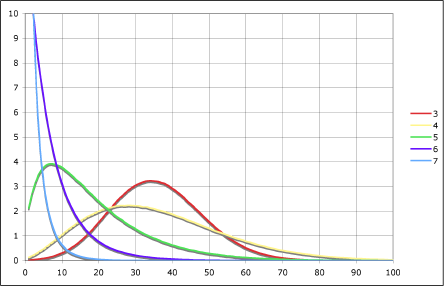
Those also look like log-normals, with four letter words being most common.

Put another way, what’s the likelihood of finding a word of a given length on a board?

Len.	Likelihood
3	99.97994%
4	99.901%
5	98.62%
6	87.56%
7	56.21%
8	21.36%
9	3.94%
10	0.442%
11	0.0362%
12	0.00228%
13	0.0001%

For context, the longest word I’ve ever found in a game was “thrashers” at nine letters.

The most common words were based on a 50,000 board sample. The graphs are based on a 5,000,000 board sample. Feel free to contact me if you’d like source or the Excel spreadsheet.

Permalink 1 Comment

Comments should be working again

Posted in meta at 5:48 pm by danvk

Turns out my Comment CAPTCHA wasn’t so smart after all. It stopped comment spam by stopping all comments. I’ve switched over to Akismet, so hopefully the comments should be working again.

Permalink Comments off

02.10.07

One Last Boggle Boost

Posted in boggle, programming at 10:24 pm by danvk

Last time, we used Tries to get a 20x speedup of an already-fast Boggle program. This time, we’ll ferret out the largest remaining bottleneck to produce an even faster Boggler.

What are the main operations that we perform in solving a Boggle board? There’s 1) word lookup, 2) checking if we’ve previously found a word, 3) checking if a letter starts a word and 4) recursion. Here’s how much time they take:

Operation	Complexity
Word Lookup	Memory access (Trie::CompletesWord)
Previously found?	Hash lookup/insertion
Starts a word?	Memory access (Trie::StartsWord)
Recursion	Subroutine call

We’re not going to do better than a memory access or a subroutine call. But who knows how long a hash lookup/insert takes? It’s O(1), but who knows what that constant factor is? It’s certainly more time than a memory access. Let’s see if we can replace that hash lookup/insert with another memory access. We’ll go through a couple of ideas.

Trie annotation
The Trie reduces CompletesWord and StartsWord to memory lookups by storing their results in each node (the is_word and children properties). So why not add another boolean property, found, to each Trie node.

This will clearly reduce the check for whether we’ve found a word to a memory access. The problem is that, if we’ve found a word on one board, we haven’t necessarily found it on the next. So when we’re done solving a board, we need to go back and clean up the Trie. That requires another data structure to track which Trie nodes we’ve marked and an extra loop to reset their found property after every board. That’s at least four memory accesses, not just one.

What’s more, this approach destroys the thread safety of the Trie. Since the Boggler can write to the Trie as well as read it, multiple solvers could easily mess each other up.

This approach works fairly well in practice, but it’s more complex than it seems at first.

Bit Vector
This is inspired by the thread safety argument against Trie annotation. Instead of storing the found bit in the Trie, why not store it somewhere else? Each thread will have a store, so thread safety isn’t an issue. This approach isn’t so different than the hash table approach we used last time, except that it uses a bit vector so it’s faster but uses more memory.

This approach has many drawbacks. First of all, how do you map pointer addresses to locations in a bit vector? There’s a lot of places that a pointer can point to, and there needs to be a bit in the bit vector for all of them. In practice, we’d measure the extent of the Trie in memory and adjust for memory alignment and the number of bits in a word. Unfortunately, you still wind up with a bit vector that’s not that much smaller than the Trie itself.

The bit vector has the same clearing problem after the board has been solved. Using bzero to clear the whole vector every time has a dramatic effect on perf, so you wind up using an extra array to track which bits you’ve set, just like the annotation strategy. This is way more complex than the first idea, but it is thread-safe.

Annotation revisited
This approach took me forever to come up with, but I think it’s the best.

Instead of annotating the Trie with a boolean found value, we can annotate it with a full 32-bit integer. The Boggler keeps track of how many boards it’s solved and stores that value in the Trie node of each word it finds. When it finds a word again, it compares the found value in that node against the board number. If they’re the same, that word has been found on this board. Otherwise it hasn’t. The beauty of this approach is that we don’t need to clean up after ourselves. It’s fine to leave a mess in the Trie, because that mess will never equal the next board number.

We’ll have to do a complete sweep of the Trie to clean out the board numbers when we overflow the board counter, but that happens only once every 2^32 = 4 billion boards, so it’s not a serious concern.

This approach is the simplest, since we don’t need any auxiliary data structures. It’s also the fastest, since we don’t have to clean up after ourselves. But it’s not thread-safe, which is its only major drawback.

The code
Here’s the new stuff in trie.h:

inline void Mark(unsigned mark) { mark_ = mark; }
inline unsigned Mark() const { return mark_; }
unsigned mark_;

We need to add a variable to count the number of boards we’ve processed in boggler.h:

unsigned num_boards_;

And here’s the goodies from boggler.cc:

void ClearMarks(Trie* t) {             // NEW
	t->Mark(0);                        // NEW
	for (int i=0; i<kNumLetters; i++)  // NEW
		if (t->StartsWord(i))          // NEW
			ClearMarks(t->Descend(i)); // NEW
}
// Returns the score from this portion of the search
void Boggler::Solve(int x, int y, int len, Trie* t) {
	prev_[x][y] = true;

	len += (bd_[x][y]=='q'-'a' ? 2 : 1);
	if (t->IsWord()) {
		if (t->Mark() != num_boards_) { // NEW
			score_ += kWordScores[len]; // NEW
			t->Mark(num_boards_);       // NEW
		}
	}

	for (int dx=-1; dx<=1; ++dx) {
		int cx = x + dx;
		if (cx<0 || cx>3) continue;
		for (int dy=-1; dy<=1; ++dy) {
			int cy = y + dy;
			if (cy<0 || cy>3) continue;
			if (prev_[cx][cy]) continue;
			if (t->StartsWord(bd_[cx][cy]))
				Solve(cx, cy, len, t->Descend(bd_[cx][cy]));
		}
	}
	
	prev_[x][y] = false;
}
int Boggler::Score(const char* letters) {
	if (!ParseBoard(letters)) return -1;

	score_ = 0;
	for (int i=0; i<16; ++i)
		Solve(i/4, i%4, 0, dict_->Descend(bd_[i/4][i%4]));

	num_boards_++;         // NEW
	if (!num_boards_) {    // NEW
		ClearMarks(dict_); // NEW
		num_boards_ = 1;   // NEW
	}
	return score_;
}

That’s about a 15 line change total. What does it buy us?

$ ./perf
Loaded 172203 words.
Testing perf on 50000 boards...
50000 boards in 4.82284 secs => 10367.35 bds/sec
Average board score: 141.1734 pts/bd

That’s another 65% speedup from last time. It’s certainly not 20x, but impressive nonetheless.

Now that we’ve got a lightning-fast Boggle solver we can solving interesting problems with it. Until next time, here’s the source.

To recap, here’s how far we’ve come:

Program	Speed	Change	Improvement
Original	.004 b/s	-	Really simple Ruby
Stems	17.5 b/s	4000x	Used stems to prune the DFS
C++	310 b/s	18x	Converted Ruby to C++
Tries	6271 b/s	20x	Use Tries instead of hashes
Final	10367 b/s	65%	Annotate the Trie with board counter

That’s a factor of six million improvement since our first try. It’s interesting to note that the final 600x of improvements all came from replacing O(1) operations with other O(1) operations.

Permalink 4 Comments

02.06.07

In which we discover that Tries are awesome

Posted in boggle, programming at 2:29 am by danvk

This is the sixth installment in an ongoing series about Boggle. See also 1, 2, 3, 4 and 5.

We’ve talked before about why Tries are the perfect data structure for solving Boggle boards. Today we’ll adapt the C++ program from yesterday’s post to use them.

Here’s a picture of part of a Trie:

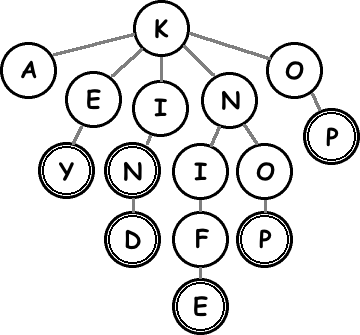
There are three important operations that we can perform quickly on a Trie node:

1. Check whether the current node completes a word
2. Check whether a particular character leads to more words
3. Descend to a child node

So, in addition to some convenience functions, our Trie interface will need to support these operations. Here’s what I came up with:

const int kNumLetters = 26;

class Trie {
  public:
	Trie();
	virtual ~Trie();
	
	// FAST access functions
	inline bool IsWord() { return is_word_; }
	inline bool StartsWord(int i) { return children_[i]; }
	inline Trie* Descend(int i) { return children_[i]; }
	
	// Slower utility functions
	void AddWord(const char* wd);
	int LoadFile(const char* filename);
	bool IsWord(const char* wd) const; // Look up a full word
	unsigned int size() const;         // Total # of words
	
  private:
	Trie* children_[kNumLetters];
	bool is_word_;
};

As you can see, the big three operations are all fast inline accessors. There’s one nuance worth talking about here: why do StartsWord and Descend take integers? In pictures of Tries, the edges are usually labeled with strings, or at least characters. This is partially a performance optimization: by mapping ‘a’..’z’ to 0..25, the program can avoid lots of annoying additions and subtractions. It also forces us to treat the ‘qu’ die specially. From now on, we’ll consider the letter ‘q’ to stand in for “qu”. We’ll have to be careful to filter words containing a ‘q’ not followed by a ‘u’ from the dictionary to make this work. We’ll also change our input interface to reflect this. Since each cell can be represented with exactly one character, there’s no reason to separate them with spaces anymore. Where we used to write “a b c d e f g h i j k l m n o p”, we’ll write “abcdefghijklmnop”. This greatly simplifies the board parsing code. I won’t go into any details, but the implementation can be found in trie.cc.

Now for the Boggler class. We’ll try to avoid changing the public interface. The only change will be the format of the boards, from “a b c …” to “abc…” The Boggler will need a Trie to contain its dictionary, but this allows us to remove the words_ and stems_ hashes. Finally, we’ll need some way to remember which words we’ve found. A hash will do fine here, but there’s some trickiness which we’ll get to below:

#include <ext/hash_set>
#include <inttypes.h>      // for uintptr_t
using namespace __gnu_cxx; // for hash_set
class Trie;

class Boggler {
  public:
	Boggler();
    int LoadDictionary(const char* filename);
	int Score(const char* bd);
	
  private:
	bool ParseBoard(const char* lets);
	void Solve(int x, int y, int len, Trie* t);
	
	hash_set<uintptr_t> found_;
	int bd_[4][4];
 	bool prev_[4][4];
	int score_;
	Trie* dict_;
};

So, what the hell is a uintptr_t? We’ll get to that in a sec. What’s more interesting is that the type signature of the recursive Solve method has changed. We no longer know what letters are in the word we’ve found so far, only its length. This is all we need to know for scoring, but it’s a little disconcerting. If we don’t know the characters in the word we’ve found, how can we tell whether we’ve found it before?

The solution is in the Trie. There’s a one-to-one correspondence between nodes in the Trie and words in the dictionary. If we’ve found a word before, then we’ve necessarily been to this Trie node before. So instead of storing the whole word in a hash, we can just store a pointer to the Trie node in its place. This is exactly the kind of dirty hack that I mentioned last time. You can do this in C/C++, but Ruby makes it rather difficult.

That leads us to uintptr_t. The STL won’t just let us put any old pointer into a hash_set. We need to convert it to something that the STL knows how to hash. On a 32-bit system, we could just use an unsigned int or long. But that won’t always work. The uintptr_t data type is an unsigned long that’s guaranteed to have the same number of bits as a pointer. So there we go.

Maybe a picture will clarify things. This shows the Boggle board on the left with all four arguments to the Solve function at each node. On the right is a part of the Trie, annotated with memory addresses. This may have also been an excuse to play with Photoshop..

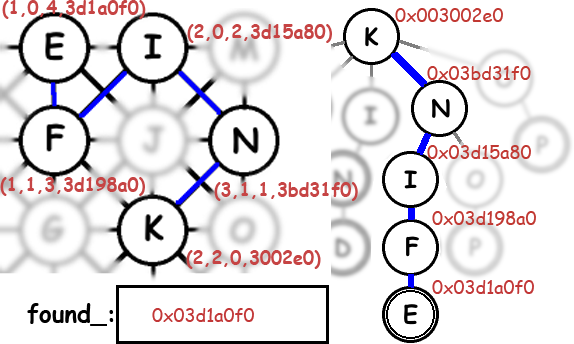
Here’s the juicy bits of the implementation:

// Returns the score from this portion of the search
void Boggler::Solve(int x, int y, int len, Trie* t) {
	prev_[x][y] = true;

	len += (bd_[x][y]=='q'-'a' ? 2 : 1);
	if (t->IsWord()) {
		// Convert the Trie node to an int and look it up
		uintptr_t hash = reinterpret_cast<uintptr_t>(t);
		if (found_.find(hash) == found_.end()) {
			score_ += kWordScores[len];
			found_.insert(hash);
		}
	}

	// Recur in each possible direction
	for (int dx=-1; dx<=1; ++dx) {
		int cx = x + dx;
		if (cx<0 || cx>3) continue;
		for (int dy=-1; dy<=1; ++dy) {
			int cy = y + dy;
			if (cy<0 || cy>3) continue;
			if (prev_[cx][cy]) continue;
			if (t->StartsWord(bd_[cx][cy]))
				Solve(cx, cy, len, t->Descend(bd_[cx][cy]));
		}
	}
	
	prev_[x][y] = false;
}

int Boggler::Score(const char* letters) {
	if (!ParseBoard(letters)) return -1;

	score_ = 0;
	for (int i=0; i<16; ++i)
		Solve(i/4, i%4, 0, dict_->Descend(bd_[i/4][i%4]));
	found_.clear();
	return score_;
}

// Board format: "bcdefghijklmnopq"
bool Boggler::ParseBoard(const char* lets) {
	for (int i=0; i<16; i++) {
		if (!lets[i] || lets[i]<'a' || lets[i]>'z')
		  return false;
		bd_[i/4][i%4] = lets[i] - 'a';
	}
	return true;
}

Now the moment of truth… what kind of performance do we get out of this? I wrapped a small binary called perf that we’ll be using to measure this from now on. It solves 50,000 pre-defined boards and reports on the time used:

$ ./perf
Loaded 172203 words.
Testing perf on 50000 boards...
50000 boards in 7.97206 secs => 6271.91 bds/sec
Average board score: 141.1734 pts/bd

That’s another 20x improvement over the previous post’s Boggler class!

Fast as this board is, there’s still one major, unnecessary bottleneck left in it. Any guesses? We’ll fix it tomorrow, at which point we’ll have a Boggler that’s about as fast as I know how to make it. Then we can start doing the fun stuff with it.

Complete source code for today’s Boggler can be found here.

Permalink Comments off