08.11.09
A Few More Boggle Examples
Hopefully the last boggle post for a while! I figured I should throw up a few more examples while I still have time left on my OmniGraffle trial.
There are two main shortcomings to the max/no mark upper bound:
- It can’t keep track of which words it’s already found.
- It can’t keep track of which choices it’s made on each cell.
These can both be fixed, but only by incurring great computational complexity. Remember the tradeoff between the “tightness” of a bound and the difficulty of computing it?
Our first example:
| t | i | . |
| {a,e} | . | . |
| r | . | . |
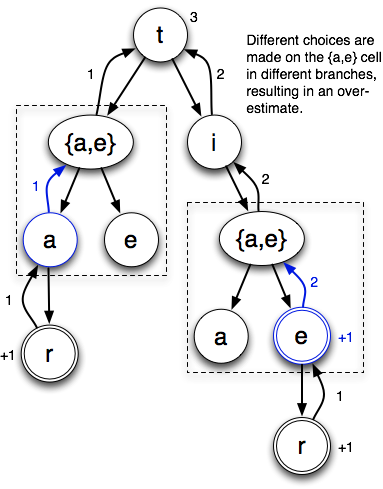
Let’s look at the search tree starting with the “t” cell. There are three possible words: “tar”, “tie” and “tier”. Here’s the search tree that max/no mark generates:
(I’m drawing the trees slightly differently than I did in the last post, to make the branching more explicit. Branches inside dotted lines come from multiple possibilities on a cell. Other branches result from the ordinary process of looking in different directions from a cell.)
In this example, max/no mark chooses the “a” when it gets to the “{a,e}” cell directly from the “t”. This makes sense, since it results in one point to the e’s zero. However, when it gets to the “{a,e}” cell through the “ti”, it chooses the “e”. This also makes sense, since it gets two points from the “e” (“tie” and “tier”) vs. zero from the “tia” prefix. By the time it makes this choice, it has no memory of choosing the “a” the last time it encountered this cell. If it did, since the “tie” prefix results in two points to the “ta” prefix’s one, it would make sense to go back and change that choice. But remembering this would require lots of expensive bookkeeping. It’s faster (but yields a looser bound) if we just accept the possibility that we’ll make different choices.
Example number 2 of max/no mark’s failings:
| t | h | . |
| h | e | . |
| . | . | . |
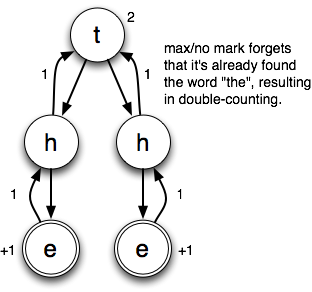
The problem in this case is that max/no mark doesn’t remember which words it’s already found. At first glance, it seems like this problem would be easy to remedy. And it certainly would on this board, in which each cell only has a single possible letter. But if you think about a board with lots of choices, you’ll start to see why it’s best to just give up and accept a looser bound.